 Precedente Precedente |
 Prossimo Prossimo |
 Indice Indice |
Paragrafo 2.
TEOREMI SCARTATI
Assioma N.1 (dell'assiomatica assiomaticità).
Un assioma è assiomatico se e solo se esprime assiomaticità indipendentemente dal fatto che
sia o no assiomatizzante.
Dimostrazione.
Assiomatica.(40)
Teorema N.1.
Preso N comunque grande, + è sempre molto pi grande.
è sempre molto pi grande.
Dimostrazione.
Dimostriamo innanzitutto che + è più grande di N, qualunque sia
N. Procediamo per assurdo: supponiamo che esista N tale che
N > +
è più grande di N, qualunque sia
N. Procediamo per assurdo: supponiamo che esista N tale che
N > + . Allora, preso k comunque grande è
k < N; ma questo è impossibile perché vorrebbe significare che
N = +
. Allora, preso k comunque grande è
k < N; ma questo è impossibile perché vorrebbe significare che
N = + , mentre si è supposto N > +
, mentre si è supposto N > + .
Quindi è vero che N < +
.
Quindi è vero che N < + , cioè +
, cioè + è più grande di N (sempre).
è più grande di N (sempre).
Dimostriamo ora il "molto". Per quanto detto nella prima parte del teorema è
N < + ; allora posso dire che esiste S tale che N + S
= +
; allora posso dire che esiste S tale che N + S
= + , ma, per quanto visto nel Capitolo Secondo e Mezzo, sarà
obbligatoriamente S = +
, ma, per quanto visto nel Capitolo Secondo e Mezzo, sarà
obbligatoriamente S = + . Quindi N è senz'altro molto più
piccolo di +
. Quindi N è senz'altro molto più
piccolo di + e dunque +
e dunque + è molto più grande, in
particolare anche per N enorme.
è molto più grande, in
particolare anche per N enorme.
Definizione N.2.
Si definisce scaritolatico un numero sufficientemente diverso da 6.
Dimostrazione.
(Ebbene s´┐Ż ci siamo voluti togliere lo sfizio di dimostrare una definizione)
Nessuno ha mai definito scaritolatico un numero sufficientemente diverso da 6, quindi la definizione
è valida (al massimo, rivolgersi alla SIAE per i diritti d'autore).
Osservazione.
Dire "sufficientemente diverso" in pratica non vuol dire
niente(41): si deve vedere caso per caso quanto
deve essere quel "sufficientemente", cioè si deve trovare il raggio dell'intorno dei numeri
non scaritolatici (raggio di non-scaritolaticità), che come ovvio ha centro in 6; chiamato
R il raggio di non scaritolaticità, abbiamo che tutti i numeri maggiori di 6+R sono
scaritolatici, cos´┐Żcome tutti i numeri minori di 6-R. Se consideriamo solo i numeri interi, quelli
presenti nell'intorno sono in numero finito, mentre quelli esterni sono ovviamente infiniti, per cui, dato
un qualunque raggio di non scaritolaticità R minore di infinito (cosa ovvia come visto nel
Capitolo sull'infinito), e scegliendo un numero a caso, la probabilità che questo sia non
scaritolatico è (casi favorevoli su casi possibili) uguale a 2R/ e
cioè è uguale a zero. Lo stesso ragionamento si pu´┐Żin realtà fare anche per i numeri
razionali e reali (mentre è impossibile con gli stati di indecisione, dato che 6 non appartiene ad
essi) per cui è dimostrato il seguente
e
cioè è uguale a zero. Lo stesso ragionamento si pu´┐Żin realtà fare anche per i numeri
razionali e reali (mentre è impossibile con gli stati di indecisione, dato che 6 non appartiene ad
essi) per cui è dimostrato il seguente
Teorema N.2.
Tutti i numeri sono scaritolatici, anche il 6.
Teorema N.3.
2+3 fa 6 per 2 abbastanza grande.
Dimostrazione.
Come è noto (!) 6 = 3 + 3 (passaggio analgebrico del 1 ordine) e utilizzando i risultati del
Capitolo Quarto si ha che 6 = 3 + 3 = 3 + 2 + 0(1). Sappiamo che 0(k) = o(k) per
k costante. Allora 0(1) = o(1) che tende a zero più velocemente di 1 (ovviamente) e
quindi 6 = 3 + 2 + o(1) = 3 + 2, essendo 2 = 2 + o(1) se 1 è abbastanza vicino a zero
oppure con un passaggio analgebrico di ordine superiore al primo e il teorema è dimostrato.
Definizione N.3.
Si definisce campo di inesistenza di f(x) l'insieme di tutti i punti in cui la funzione non è
definita, nè definibile, nè tantomeno derivabile, integrabile, invertibile, isomorfabile,
iniettabile, suriettabile ecc. ecc.
Definizione N.4.
Si definiscono porcherie tutte le definizioni del tipo della precedente.
Si osservi che non era necessario che la N.3 venisse prima della N.4; in luogo della N.3 andavano bene anche altre definizioni. Abbiamo infatti il
Dilemma N.1.
Date le definizioni N.3 e N.4 come sopra, la N.3 pu´┐Żessere sostituita da una qualunque definizione di
questo libro (e magari anche di qualcun altro).
Coronaria N.1 (non si sa bene coronaria a cosa).
La quantità al primo membro dell'equazione precedente è uguale a sin(x)/x3 a
meno di una costante.
Dimostrazione.
Non siamo riusciti a trovare l'equazione precedente, probabilmente di qualche teorema di cui la presente
è coronaria. Se ci saranno ulteriori sviluppi vi terremo informati.
Diamo adesso tre formulazioni differenti dello stesso teorema che di volta in volta risulteranno utili nello studio di funzioni.
Teorema N.4.
Una funzione f(x) è convessa in un intervallo (a, b) in cui è continua e
derivabile almeno due volte e in cui la derivata seconda non cambia segno, se nello stesso intervallo non
è nè costante, nè concava.
Dimostrazione.
E senn´┐Żche cavolo è?!
Teorema N.5.
Una funzione f(x) è convessa in un intervallo (a, b) in cui è continua e
derivabile almeno due volte e in cui la derivata seconda non cambia segno, se nello stesso intervallo non
è nè costante, nè concava, nè discontinua, nè disintegrabile, nè
ricopribile, nè questa, nè quell'altra cosa, ma è convessa.
Teorema N.6.
Una funzione f(x) è convessa se e solo se è convessa.
Definizione N.5.
Una discontinuità è detta di terzo tipo se non è nè di primo nè di
secondo, per´┐Żsi ostina ugualmente ad essere discontinua (cioè è continuamente
discontinua nel tempo).
Teorema N.7 (dei tre carabinieri).
Se ho tre funzioni f(x), g(x), h(x) tali che f(x) > g(x) > h(x) per ogni x  R e so che per x che tende a infinito f(x) e g(x) tendono allo stesso limite N, non posso dire con
precisione a cosa tende h(x) (per´┐Żso che non è meno di N).
R e so che per x che tende a infinito f(x) e g(x) tendono allo stesso limite N, non posso dire con
precisione a cosa tende h(x) (per´┐Żso che non è meno di N).
Dimostrazione.
Non ci sentiamo proprio in dovere di dimostrare questa robaccia, al massimo se qualcuno è convinto
del contrario ci dica, dando una dimostrazione plausibile, come farebbe a trovare il limite di
h(x).
c.n.v.d.(42)
 Figura N.1 - Il teorema dei tre carabinieri. |
Definizione N.6.
Una funzione f: A  R si dice lipschitziana se esiste una costante M > 0
tale che
R si dice lipschitziana se esiste una costante M > 0
tale che  f(x) - f(y)
f(x) - f(y) 
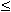 M
M  x - y
x - y  per ogni x,y
per ogni x,y  A.
A.
Solo un'osservazione: questa definizione è serissima ed è stata presa da un
libro di Analisi I, ma dato che il termine lipschitziana sa tanto di Analisi N, non abbiamo resistito
alla tentazione di includerla.
Teorema N.8.
Una funzione lipschitziana è uniformemente continua.
Dimostrazione.
È troppo seria per gli scopi di questo Paragrafo (e di questo testo in generale); si rimanda la
dimostrazione ai tomi di Analisi I e II.
Definizione N.7.
Si definisce fattore di potenza un qualunque contadino della
Basilicata(43) (basta che abbia visto almeno
una volta Potenza nella sua vita).
Assioma N.2.
L'Errore Globale è SEMPRE enorme (anche se è zero).
(40) Notare il tentativo di dimostrare un assioma...
(41) è una soggettività (vedi Capitolo Secondo).
(42) Come Non Volevasi Dimostrare.
(43) Per gentile concessione di
Gino Bramieri .
.
 Precedente Precedente |
 Prossimo Prossimo |
 Indice Indice |