Capitolo 5, "I passaggi analgebrici"

Paragrafo 4.

PROPRIETÀ DEI PASSAGGI ANALGEBRICI

Come preannunciato, esiste un teorema in grado di spiegare il fatto che ogni ordine di passaggi analgebrici (non dimentichiamoci che gli ordini sono anche insiemi) include tutti i suoi precedenti. Il primo ordine è dunque incluso in tutti gli altri, il quinto li include tutti. L'importanza del teorema è nota dal Paragrafo precedente: ogni problema risolubile con passaggi analgebrici di un dato ordine è anche risolubile con quelli degli ordini superiori, ma non è sempre vero il contrario (e qualche volta nemmeno il contrario del contrario, ma noi non l'abbiamo detto).

Teorema 5.4 (di inclusione).
Ogni ordine di passaggi analgebrici è incluso nel suo successivo, ma non coincide con esso.

Dimostrazione
[La dimostrazione è riportata (tradotta dal dialetto scozzese) così come McBowd l'ha formulata; alcuni tratti non rilevanti sono stati omessi per non appesantirla, N.d.A.].
Per quanto riguarda i primi due ordini, la dimostrazione è palese. Per dimostrare che gli ordini dal secondo al quinto sono inclusi l'uno nell'altro, facciamo ricorso ad un artifizio. Poniamo _i= ordine i-esimo, _i-1 = ordine i-menounesimo, per i = 2, .., 5. Essi sono ovviamente degli insiemi, le cui cardinalità poniamo siano k_i e k_i-1. La sommatoria

è senz'altro una sommatoria interessante; tenendo conto di ciò e del fatto che

è abbastanza infinito si deduce che (...) possiamo stabilire delle relazioni tra le cardinalità dei vari ordini e precisamente

k_i-1 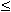k_i.

Ciò non fa altro che aumentare il sospetto che _i-1 _i. Ma i sospetti, come ben sappiamo, non bastano a confermare i fatti. Allora proseguiamo nell'artifizio: noto il valore di , diciamo che se a è un elemento di _i allora a potrebbe esserlo o non esserlo, previa definizione di cosa sia a. Il punto è che a, dato che (...) è sufficientemente grande, è un elemento di _i-1. Resta da dimostrare che anche a è elemento di _i-1, ma ricordando le proprietà di controbilanciamento degli assiomi esuli di Kronsky che indicano (...) cose vere, si ha proprio che a appartiene a _i-1, da cui la tesi, poiché a è generico.

Resta ora come ultimo scoglio la dimostrazione che l'insieme dei passaggi analgebrici è un campo, con tutte le conseguenze che ne derivano. Per coloro che non ricordano l'Algebra (sappiamo essere pochissimi) riportiamo la definizione di campo e alcuni preliminari necessari alla comprensione del teorema. Per queste persone che o non hanno mai avuto a che fare con l'Algebra pura o la odiano a tal punto da averla studiata per costrizione fisica e poi dimenticata nell'oblìo o per chissà quali filosofici motivi non la considerano nemmeno una scienza esatta, rammentiamo che l'Algebra è quella materia che

abbonda di lettere per trascurare i numeri;
aborrisce il campo reale in quanto continuo, preferendogli i numeri interi, relativi e razionali con le loro spigolosità; con ciò, non crediate che le cose migliorino nel senso di semplificarsi, anzi;
si basa sul cosiddetto principio delle scatole cinesi: ogni definizione, anche la più stupida, può essere espansa in una enorme, sostituendo ad ogni parola la sua definizione e così via ricorsivamente; è noto che il tempo trascorso prima di giungere al Vocabolario è proporzionale alla distanza della definizione di partenza dalla pagina 1 del libro di Algebra (proporzione esponenziale, di solito);
sfrutta a più non posso il teorema di complicatizzazione (vedi Capitolo Settimo).

Il punto 3 si estrinseca ottimamente nelle definizioni che seguono, utili agli studenti di cui sopra per procedere nella comprensione del teorema di campo. Si è volutamente tralasciata la definizione di struttura algebrica, per non appesantire la trattazione, ma soprattutto perché proprio non ne avevamo voglia.

Definizione 5.2 (semigruppo).
Una struttura algebrica (S, *) costituita da un insieme S e da un'operazione binaria * su S, si dice semigruppo se * è associativa.
Se * ammette unità (bilatera), il semigruppo (S, *) si dice monoide.

Associativa significa che (a*b)*c = a*(b*c), con che sappiamo che le parentesi sono molto utili anche quando non servono.
L'unità è quella cosa strana indicata con 1 tale che se si fa 1*a, con a qualunque, si ottiene ancora a. Bilatera sta a significare che 1*a = a*1 = a, infatti, per qualche malaugurato motivo, può essere che 1*a sia diverso da a*1; questo per le ragioni riportate al punto 4, ma anche per qualcun'altra.

Definizione 5.3 (gruppo).
Un semigruppo (G, *) si dice gruppo se:

ammette unità;

per ogni elemento di G esiste il suo inverso.

L'elemento g G ammette inverso q G se g*q = q*g = 1. Anche qui l'inverso si è supposto bilatero... onde evitare imprecazioni.

Definizione 5.4 (anello).
Una struttura algebrica (A, +, ) costituita da un insieme A e da due operazioni binarie + e su A, si dice anello se:

(A, +) è un gruppo commutativo;

(A, ) è un monoide;

per ogni a, b, c, appartenenti ad A si hanno le proprietà distributive: a(b + c) = ab + ac
(b + c)a = ba + ca

Commutativo è bello, commutativo piace: vuol dire che a*b = b*a per ogni a e b. Se un gruppo è commutativo è bello, altrimenti no.
Per quanto riguarda le proprietà distributive sono altrettanto belle e piacciono, ma con discrezione poiché sono più lunghe da ricordare.
Ed ora, l'agognato termine. Per la cronaca, unitario significa "che ammette inverso".

Definizione 5.5.
Un anello commutativo (K, +, ), con almeno due elementi, si dice campo se ogni elemento di K, diverso da zero è unitario.

Finalmente, la tanto sospirata definizione è giunta ai nostri occhi. Ci si chiederà: ce n'era bisogno? La risposta è probabile che sia una funzione di probabilità... con una spiccata tendenza ad assumere valori elevati di probabilità per la risposta NO, ma non curiamocene e sospiriamo felici di essere giunti quasi in fondo al Capitolo. Siamo pronti all'enunciazione del

Teorema 5.5 (di campo).
L'insieme dei passaggi analgebrici è un campo.

Dimostrazione.
Si tratta di dimostrare che detto insieme gode di tutte le proprietà dei campi, quindi: dev'essere un anello, deve avere almeno due elementi e ogni elemento diverso da zero deve ammettere inverso.
Che abbia almeno due elementi è abbastanza chiaro, così come che ogni passaggio ammette inverso, ovvero: se applico un passaggio ad una formula posso sempre tornare indietro, quindi in realtà è come se non mi fossi affatto mosso dalla formula di partenza; ho dunque applicato il passaggio algebrico inverso e trovata l'unità. L'unico elemento a non ammettere inverso deve essere lo zero. Cerchiamo l'elemento zero dell'insieme. Esso sarà, per definizione di zero, l'elemento 0 tale che a*0 = 0*a = 0: esso è quindi il passaggio algebrico del secondo ordine che moltiplica per 0 tutto quello che trova (detto anche Metodo dell'Assorbimento, Capitolo Terzo).
Ora resterebbe da dimostrare che l'insieme dei passaggi analgebrici è un anello. Tale dimostrazione è abbastanza ovvia e lasciata al lettore per esercizio.

ESERCIZI.
5.6. Per dimostrare l'ultima parte del teorema 5.5 occorre dimostrare che sull'insieme dei passaggi analgebrici si possono definire due operazioni + e in modo da costruire una struttura algebrica (che si dimostrerà poi essere un anello). Come possiamo definire queste due operazioni ?

per mezzo del teorema fondamentale dell'Algebra
per mezzo del teorema fondamentale dell'Analisi
per mezzo del teorema fondamentale dell'Analisi N
per mezzo del teorema fondamentale della Statistica
per mezzo della teoria della Relatività Generale
per mezzo della Despotizzazione Triquantizzata.

5.7. Si individui un isomorfismo tra l'insieme dei passaggi analgebrici e lo spazio di indecisione.
5.8. Si rienunci la dimostrazione del teorema 5.4 (di inclusione) sulla base del teorema fondamentale dell'Analgebra riportato nello scritto di McBowd al Paragrafo 1. La rienunciazione, per semplicità, può essere eseguita in dialetto scozzese.

Prossimo

Indice