tux Torna alla home page Introduzione all'Analisi N
Precedente Prossimo Indice

Paragrafo 2.

TEORIA NORMALE DEGLI ERRORI.

Abbiamo osservato nel paragrafo precedente come le nozioni di errore assimilate dalla teoria comune siano insufficienti per i nostri scopi. A causa però degli argomenti che saranno introdotti non sarà inutile un ripasso della terminologia e degli strumenti a disposizione: nel contempo, a questi dati che dovrebbero essere acquisiti da tempo (chissà perché si presume sempre che un povero disgraziato sappia tutto prima che qualcuno glielo spieghi...) saranno aggiunti nuovi concetti indispensabili.
Data una quantità (canonica) diremo che una misura di questa quantità è affetta da un errore se essa si discosta dalla quantità teorica di un valore E. Se a è il valore effettivo e A quello misurato, allora E = a-A è detto errore assoluto. Esso, insieme all'errore relativo e, dovrebbe essere noto fin dagli studi secondari. Se cosí non fosse, non importa, tanto a noi non ci fregano tanto gli errori assoluto e relativo, quanto gli errori definitivo e totale.

Definizione 4.2.
Si definisce errore definitivo, (e non è un gioco di parole) l'errore ottenuto "da un certo punto in poi" (qualunque cosa voglia significare).

Definizione 4.3.
Si definisce errore totale (o ideale) l'errore massimo raggiungibile per una quantità.

L'errore totale è raramente raggiungibile tranne che in alcuni casi particolari, o meglio, diciamo, di particolare gravità. Si osserva infatti che in tutte le situazioni in cui si rende necessario un contenimento dell'errore è molto probabile che l'errore globale venga raggiunto. Questo a causa in primo luogo del Teorema e in secondo luogo, invece, ancora per il Teorema.
Altre caratterizzazioni che dovrebbero essere note sono: o (o-piccolo), O (o-grande), (asintoticità). Per completezza riportiamo anche queste nella schematizzazione che segue per poter poi effettuare utili confronti con le nuove nozioni che verranno introdotte.

Siano f(n) e g(n) due funzioni di n, entrambe definite su un insieme A; diremo che:

  1. f(n) = o(g(n)) (f(n) è o-piccolo di g(n)) se lim f(n)/g(n) = 0 per n.
  2. f(n) = O(g(n)) (f(n) è o-grande di g(n)) se esiste k < tale che f(n)/g(n) 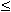k in un intorno di un punto oppure per n.
  3. f(n) = 0(g(n)) (f(n) è o-medio di g(n)) se f(n) è piú o meno vicina a g(n) in un intorno di un punto o per n. In particolare 0(k) = o(k) per k costante.
  4. f(n) = (g(n)) (f(n) è o-riale di g(n)) se f(n) è sempre MOLTO piú grande di g(n) in un intorno di un punto o per n.
  5. Data una funzione f(n) nella variabile n, si dice che S(n) è un annullamento di f(n) se S(f(n) = 0 per ogni n(22), mentre S(n) è una sovraelongazione di f(n se S(f(n)) = (f(n)).

Riveste una certa importanza nell'ambito dello studio degli errori il

Teorema 4.1.
Sia f(x) una funzione qualunque di variabile qualunque; se x non è fissato a priori, f(x) è una quantità non quantificabile.

La dimostrazione è evidente e lasciata per esercizio. Si noti che non è vero il contrario, cioé se x è fissato non è detto che f(x) sia quantificabile; occorre studiare la funzione e stabilire se restituisce valori inconsulti o meno. In generale sarà vera la prima ipotesi (cioé i valori inconsulti), poiché la grande maggioranza delle funzioni studiate è di variabile reale (N, Z, Q e soprattutto C fanno molto piú senso) e la stragrande maggioranza delle funzioni non ha variabili nè in R, nè in Z, nè in N, nè in Q e nemmeno in C (che come ultima spiaggia potrebbe anche andar bene anche se, essendo CRxR, raddoppierebbe i problemi che abbiamo in R), ma in altri campi che spesso e volentieri non sono campi, ma aborti matematici o peggio ancora non matematici, quali nemmeno il buon McBowd con i suoi passaggi analgebrici (vedi) avrebbe il coraggio di considerare.
Tornando alle definizioni di o-piccolo, o-medio, o-grande, ecc. si può dimostrare che questi simboli rappresentano quantità non quantificabili non solo per x non noto a priori, ma anche predeterminato. Difatti: che diavolo significa o(1) ? Si ha la quasi-validità del

Dilemma 4.1.
Sia f(x) una funzione a variabile reale; allora o(f(x)) = (O(f(x))). Inoltre, sia k una costante, k R: allora (k) = o(k).

La dimostrazione si emunge da considerazioni di carattere demagogico e comunque esula dagli scopi di questo libro(23). Si rimanda alla bibliografia per ulteriori delucidazioni.

(22) funzioni di questo tipo sono comunemente dette "funzioni inutili".

(23) un modo molto elegante per dire che non sapremmo dimostrarvi proprio un bel tubo.

 

Precedente Prossimo Indice