 Precedente |
 Prossimo |
 Indice |
Paragrafo 2.
CONFRONTO TRA INFINITI
Secondo la logica 
1 = ma anche
2 = ; questo in realtà non è all'apparenza
molto logico, anche se non si può nemmeno dire che sia illogico. Soffermiamoci sulla prima
uguaglianza, cioè 1 = , cosa vuole dire questa
espressione? Infinito può essere una qualunque funzione F(x) che cresce
indefinitamente per x che tende a qualcosa; prendiamo come esempio 1/x per
x
0, per cui possiamo scrivere che per x0,
1/x 1 = 1/x, ma in realtà nel compiere il prodotto di 1/x per 1 al primo membro,
si è perso un po' di tempo, che non risulta perso al secondo membro, per cui considerando che per
ogni x ci vuole più tempo a sinistra che a destra, e tendendo x a zero, ci troveremo
presto ad avere un F(x) discretamente maggiore a destra rispetto alla sinistra, per cui
possiamo senz'altro dire che 1/x1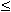 
1/x la quale relazione, continuando a
decrescere il primo membro con x diventa diseguaglianza stretta. In realtà questo esempio
è del tutto generale (la dimostrazione, semplice ma un po' lunga, viene lasciata come
esercizio-tortura al lettore), di conseguenza possiamo scrivere, tenendo conto subito della disuguaglianza
stretta, che 1 < , dove per
si intende, come visto sopra, una qualunque funzione che tende a infinito.
In determinati tipi di funzioni, dette a ritardo costante, si può
applicare a destra un fattore moltiplicativo leggermente diverso da 1, detto fattore di rincorsa,
in modo da bilanciare il ritardo della x; il fattore di rincorsa si indica di solito con
per cui si ha, se tutto va bene, che F(x)
= F(x), con > 1 e x che tende a qualcosa in modo che
F(x) tenda a infinito. Dato però che il ritardo della x al primo membro cresce
al crescere di x stessa, per la maggior parte delle funzioni non si riesce a trovare un fattore di
rincorsa costante; infatti in generale questo dipende dal valore di x e si può dimostrare che
per ogni funzione F(x) che tende in qualche modo a infinito, è possibile trovare una
funzione di rincorsa, dipendente anch'essa da x, chiamata di solito
(x) (15) e che, nel caso
di una funzione a ritardo costante, è una funzione costante, strettamente monotona crescente e il
cui valore iniziale(16) è sempre uno; questa
funzione ci permette di scrivere in modo del tutto generale, qualunque sia la F(x) che
rispetta le ipotesi, che F(x) (x) = F(x), per
x che tende a un valore tale per cui la F(x) diverge a infinito. L'uguaglianza
precedente prende il nome di uguaglianza di Scarr Afò, dal nome del gatto del suo
scopritore.
È ora perfettamente deducibile dalle cose dette sopra (in caso in fase di stampa
questa sia la prima riga di una nuova pagina, il "sopra" va inteso in modo più temporale
che spaziale) che 2 non è esattamente il doppio di infinito, cioè
si ha 2 < 2, sia per le funzioni a ritardo costante che
per le altre; si lascia come esercizio la discussione di come si possano sfruttare il valore
o la funzione (x) calcolati in precedenza anche in
questo caso.
ESERCIZI.
2.1. Generalizzare completamente il discorso sulle funzioni di rincorsa (e sui fattori di rincorsa) per un
N qualsiasi in modo da mantenere l'uguaglianza N =
N.
2.2. Spiegare in modo chiaro e conciso perché tutto quello detto sopra non ha senso.
(15) Teniamo conto che il calcolo stesso
della funzione (x) necessita di tempo per essere svolto, tempo da aggiungere
a quello del successivo prodotto per x e di tutto questo la stessa (x)
deve tener conto.
(16) Non si sa bene iniziale rispetto a cosa.
| Precedente |
Prossimo |
Indice |